ゲーム理論（二人・二択）の混合戦略の確率求め方

ゲーム理論については前回の記事で触れましたが、今回の記事はその続きです。

今回の記事では、混合戦略の確率の求め方について、詳細を書いていきます。

混合戦略は、何度も同じゲームを繰り返す場合において、相手がどのような確率で選択肢を選んだとしても、全ゲームで得られる平均の利得を一定にすることを意図したものです。
長期的な目で見て、利得が下がるリスクを最も軽減できる戦略です。

この戦略の実現方法について直感的に書くと、リスクの高い選択肢（相手が選ぶ選択肢によって利得が大きく変わる選択肢）を選ぶ確率を少なめに、リスクの低い選択肢（相手が選ぶ選択肢によって利得が大きく変わるらない選択肢）を選ぶ確率を多めにすると、混合戦略に近くなります。

各選択肢の選択確率を正確に求めるには、連立方程式や微分方程式等を用いて計算を行う必要があります。
今回の記事では以下の前提で計算を行います。

• 劣等戦略（相手がどのような選択肢を選んだとしても、他のある選択肢以下の利得しか得られない選択肢）はあらかじめ除外
• プレイヤーが二人で、選択肢は二択のゲームを想定

【今回の例で取り扱う利得表】

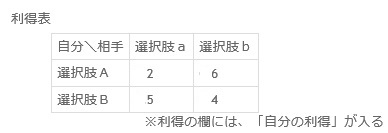
【混合戦略の求め方】

１．連立方程式を解く方法

選択肢Ａを選ぶ確率をp、選択肢Ｂを選ぶ確率を1-pとおく。
混合戦略が成り立つ時、相手が選択肢ａを選んだ場合の期待利得と相手が選択肢ｂを選んだ場合の期待利得は等しくなるため、以下の式が成り立つ。

以上より、選択肢Ａを選ぶ確率が0.2、選択肢Ｂを選ぶ確率が1-0.2(=0.8)の時に、混合戦略となる。

２．微分方程式を解く方法

選択肢ａが選ばれる確率pが決まる時、選択肢ｂが選ばれる確率は1-pという形で一意に求まる。
また、混合戦略の定義は、「相手が選択肢ａを選んだ場合の期待利得と相手が選択肢ｂを選んだ場合の期待利得が等しくなるように選択肢を選ぶ」である。
そのため、混合戦略の定義は、「相手が選択肢ａを1の確率で選ぶ場合の期待利得と相手が選択肢ａを1-1(=0)の確率で選んだ場合の期待利得が等しくなるように選択肢を選ぶ」と置き換えることができる。

そこで、相手が選択肢ａを選ぶ確率をx軸、自分の利得をy軸に置くと、以下のグラフを得られる。
下記のグラフについて、線分Ａ-Ａ’は選択肢Ａを選んだ場合の利得、線分Ｂ-Ｂ’は選択肢Ｂを選んだ場合の利得、線分Ｃ-Ｃ’は混合戦略となる場合の利得を示している。

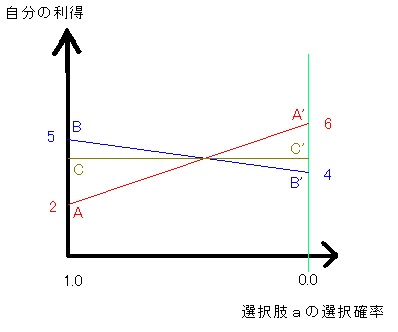
線分Ａ-Ａ’と線分Ｂ-Ｂ’を式に表すと以下のようになる。

線分Ａ-Ａ’と線分Ｂ-Ｂ’を微分し傾きを求めると、以下のようになる。

ここで、線分Ｃ-Ｃ’は混合戦略であり、xの値によらずyは一定のため、傾きは0である。
線分Ａ-Ａ’をpの比率で、線分Ｂ-Ｂ’を1-pの比率で合成し、線分Ｃ-Ｃ’を生成する場合、比率pは以下の式で求まる。

以上より、選択肢Ａを選ぶ確率が0.2、選択肢Ｂを選ぶ確率が1-0.2(=0.8)の時に、混合戦略となる。

【検算】

選択肢Ａを選ぶ確率が0.2、選択肢Ｂを選ぶ確率が0.8の時の期待利得を求める。

相手が選択肢ａを選んだ場合、自分の期待利得は以下のようになる。

相手が選択肢ｂを選んだ場合、自分の期待利得は以下のようになる。

①と②が等しいため、選択肢Ａを選ぶ確率が0.2、選択肢Ｂを選ぶ確率が0.8の時に混合戦略となる。

【混合戦略の簡単なイメージ】

教育機関で教えられるのは連立方程式を解く方法で、複雑な状況に対応することを考えるとこちらの方法を用いるべきです。
しかし、プレイヤーが二人で選択肢が二択というような簡単な状況では、微分方程式を解く方法の方が簡単にイメージできます。

傾きを合成して0にするだけなので、簡単に書いてしまうと「選択肢Ａの傾き:選択肢Ｂの傾き*-1」の逆数がそのまま「選択肢Ａを選ぶ確率」と「選択肢Ｂを選ぶ確率」になります。
上記の例で言うと、「4:1」の逆数「1/4:1」=「1:4」=「0.2:0.8」が「選択肢Ａを選ぶ確率」と「選択肢Ｂを選ぶ確率」になります。
手続き型のプログラムで計算できるように計算式を書くと、以下のようになります。

---

いかがでしたでしょうか。

今回の記事では、前回の記事では簡単にしか触れなかった混合戦略について、詳しく書いていきました。
実際にゲーム理論を応用する場合は、数字や確率で状況を表すことが難しい場合が多いので、「リスクの高い選択肢を選ぶ確率を少なめに、リスクの低い選択肢を選ぶ確率を多めにする」という直感的な理解で問題無いと思います。

ゲーム理論を現実世界に応用する際には、いくつかの注意点があります。
それを、今後の記事で書いていきたいと思います。