私が2進数や16進数を説明する時に使っている図はこれです。
基数計算を本質的に理解できる図になっていると思います。
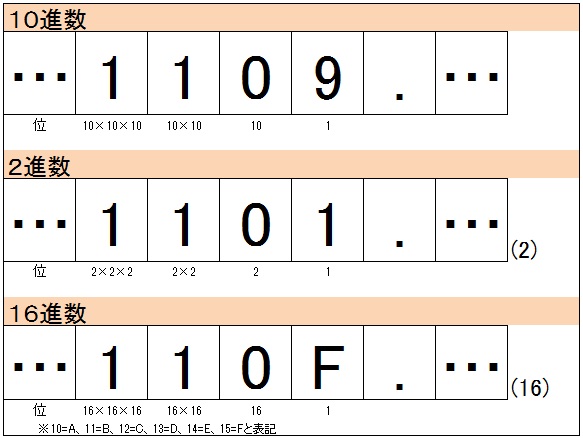
私たちが日常で使っているのは10進数です。
10に達すると次の桁に繰り上がるという概念です。
対して、2進数は2に達すると次の桁に繰り上がるという概念であり、ビットのON/OFFの2値で制御するコンピューターにとっては2進数の方が都合が良いです。
16進数は16に達すると次の桁に繰り上がるという概念であり、2の倍数となっている(16進数2桁で256通り=8ビット=1バイトの情報を扱える)ため、これもコンピューターにとっては都合が良いものになっています。
「○進数は○に達すると次の桁に繰り上がるという概念である」ということさえ覚えておけば、特に困ることはないと思います。 少なくとも私は、仕事でも趣味でも資格試験でも困ったことはないです。
基数計算は以下のように行います。
例えば、125を10進数で表す時は
- 10*10*10の桁…1000より小さいのでここには何も入らない。
- 10*10 の桁…ここを1にすれば、125の内100は表現できる。残り25。
- 10 の桁…ここを2にすれば、25の内20は表現できる。残り5。
- 1 の桁…ここを5にすれば、残りの5を全て表現できる。
→125
と表すことができます。
2進数もこれと同じです。
例えば、7を2進数で表す時は
- 2*2*2の桁…8より小さいのでここには何も入らない。
- 2*2 の桁…ここを1にすれば、7の内4は表現できる。残り3。
- 2 の桁…ここを1にすれば、3の内2は表現できる。残り1。
- 1 の桁…ここを1にすれば、残りの1を全て表現できる。
→111(2)
と表すことができます。
いかがでしたでしょうか。
参考書では、以上のような説明がされることは意外と少ないと思います。
何かを説明する時に、色々な角度で説明すると理解が深まる場合があるので、今回は独自の角度での説明を書いてみました。
参考になれば幸いです。



コメント